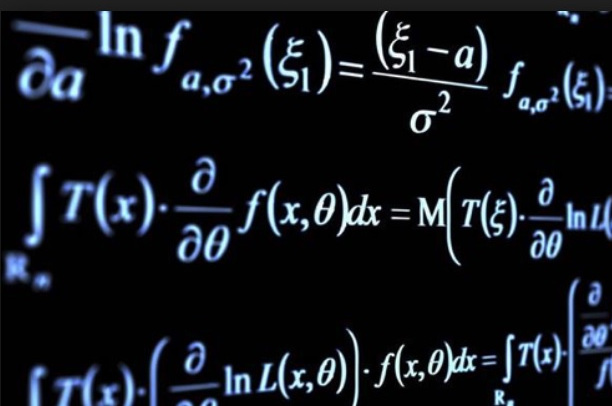
数学上の「平均計算」の三種類（相加平均,相乗平均,調和平均）について、見てみる。

平均というと、計算方法は「全て足して、その個数で割る」と計算する。確かにこれが一番分かりやすい平均計算だと思う。しかし、これは「平均」の一種類でしかない。平均という計算方法について、代表的な三種類を挙げてみて数学の世界を見てみたい。

１．平均の計算とは

平均の計算と言えば「足して割る」というのが、誰もが思いつく計算と思う。一般的にはその計算で「平均」と語られるが、ひとくくりに平均と言ってもいろんな計算がある。

単純に足して割る、というのは、公平に見えるがそうとも言い切れない。「50」と「50」の平均は「50」であるが、「0」と「100」の平均も「50」である。確かに平均は同じ「50」だが、その内容は全く異なる。例えば、学校のクラスが２つあって、「50点を取る生徒が30人いるクラス」と、「100点を15人、0点を15人の生徒が取るクラス」があったとき、その２つのクラスは平均点は同じだが、果たして勉強のやり方は同じでいいのだろうか？

あくまで一般的に言われている平均計算というのは、「相加平均（arithmetic mean）」のことである。一番理解しやすい平均計算として捉えるべきで、これだけがいわゆる「平均」ではない。

２．三種類の平均計算

平均の計算にはいろいろあるが、ここではその平均の仕方そのものの区分により「相加平均（そうかへいきん）」と「相乗平均（そうじょうへいきん）」と「調和平均（ちょうわへいきん）」の三種類を紹介したい。

①　相加平均そうかへいきん（arithmetic mean)

いわゆる平均。計算式は至ってシンプルであり、要素を足して数で割る、というものである。
※　aとbの「相加平均」
$$(相加平均)=\frac{a + b}{2}$$
※ \(x_1\)～\(x_n\)の「相加平均」
$$(相加平均)=\frac{x_1 + x_2 + ・・・+x_n}{n}$$

②　相乗平均そうじょうへいきん（geometric mean）

平均する数値を乗じて、その数（ｎとする）の分だけの「ｎ乗根」を取るものである。計算式は以下の通り。
※ aとbの「相乗平均」
$$(相乗平均)=\sqrt{a × b}$$
※ \(x_1\)～\(x_n\)の「相乗平均」
$$(相乗平均)=\sqrt[n]{x_1 \times x_2 \times ・・・\times x_n}$$

③　調和平均ちょうわへいきん（harmonic mean）

これは少しわかりにくい平均計算と言える。言葉で言うと、「逆数の平均の逆数」となる。計算式は以下の通り。
※ aとbの「調和平均」
$$(調和平均)=\frac{1}{\displaystyle\frac{1}{2} \times (\displaystyle\frac{1}{a} + \displaystyle\frac{1}{b})}$$
※ \(x_1\)～\(x_n\)の「調和平均」
$$(調和平均)=\frac{1}{\displaystyle\frac{1}{n} \times (\displaystyle\frac{1}{x_1} + \displaystyle\frac{1}{x_2}+ ・・・ +\displaystyle\frac{1}{x_n})}$$

３．違いは何か？

一般的に使われるのは、やはり相加平均と思う。それが平均であることは一番説明しやすいし納得しやすい。しかし、「相加平均」だけでは正しく傾向をつかむことができない場合がある。例えば下記の場合を見てみたい。

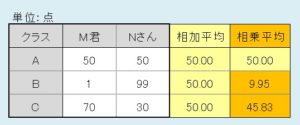
(1) ２人のグループが３つあるときの「平均」点は？

下記の例で、「相加平均」と「相乗平均」の違いを見てみたい。

上記を見てどう思うだろうか？「どちらが平均として正しいのか」の問題ではない（そんな問題に答えはないが）。「平均」という計算の特色が色濃く見えることを分析したい。

上記の通り、すべて「相加平均」上は50点である。しかし、その中身は全然違う。グループごとに大きく特色が出ている。そこで「相乗平均」による平均を並べてみることで、その傾向が少し見えてくる。グループBは10点にも満たない平均となる。グループCは50点に近い。
相乗平均は「偏差」と近い性格を持つ。その数値が、相加平均と離れれば離れるほど、ばらつきが大きいといえるだろう。

(2) 調和平均の活用は？

調和平均が語られるときによく言われるのが、速度の問題である。

これを見た時に、まず相加平均による平均時速を見てみる。
$$（相加平均） = \frac{ 100 + 60}{2} \\　　　　　　 = 80[km/h]$$

このように、相加平均を用いれば80km/hとなる。しかし、このときに「平均」をどのように捉えるべきか考えてみたい。行きには時速100kmで移動し、帰りは時速60kmで移動している。ということは、行きと帰りとで移動時間は大きく異なる。その上で、平均時速の計算はどうあるべきか、それは「平均」に何を求めるかによると思う。その移動時間も考慮した計算となると「調和平均（harmonic mean）」が最適となる。
それでは、「調和平均」による平均時速を見てみる。
$$（調和平均）=\frac{1}{\displaystyle\frac{1}{2} \times (\displaystyle\frac{1}{100} + \displaystyle\frac{1}{60})}\\　　　　　　 ＝ 75[km/h]$$
「調和平均」だと行きと帰りの時間の変化も考慮される。100km/hで移動した行きより、帰りの方が時間が長い。そのため、帰りの時間が長い面を加味した「調和平均」の平均時速は、「相加平均」より小さくなるのである。

４．平均計算に見る数学の使い方