AIにも応用される「ベイズの定理」を見ると共に、例題を通じてPCR検査による罹患率を計算してみる。
「ベイズの定理」というのをご存知だろうか。高校数学で学ぶと言われるこの考え方は、今話題の武漢コロナの「PCR検査」を考える上でうってつけである。また、AIにも広く利用されている数学の理論である。そのほんの最初の入り口を見ていきたい。是非、お付き合いを。
ページ目次
1.ベイズの定理とは
高校数学で学ぶ「ベイズの定理」は、単純だが非常に興味深い「定理」である。人工知能(AI)の基礎となる、機械学習やディープラーニング(深層学習)にも応用される定理である。
内容の前に、「ベイズの定理」の歴史に触れておきたい。UK(イギリス)のロンドンに住む牧師で数学者のトーマス・ベイズが証明したと言われるが、それが日の目を見たのは彼の死後だった。トーマス・ベイズは1700年代の人で、ベイズの定理はなんと300年も前の物ということになる。
このベイズ定理を使って、「ベイズ推論」といわれる考え方があり、また統計学にも応用され「ベイズ統計」と言われるものもある。またベイズ推論はAIの考え方の基礎である「機械学習」にも使われる。そしてその応用の「ディープラーニング」にも利用される。
ベイズ推論やベイズ統計には、複雑な積分など、高等数学が必要という。ここではそんなベイズ定理を、ほんの入り口だけ、具体的な数式と計算例と共に見ていきたい。
2.ベイズの定理の数式
(1)まずは「条件付き確率」について
ページ目次 [ 開く ]
ベイズの定理は「条件付き確率」の変形である。そのためベイズの定理には、「条件付き確率」を理解しないといけない。
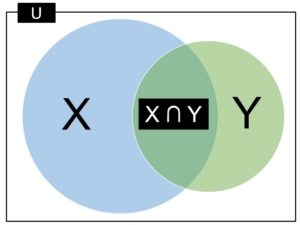
「条件付き確率」は下記の式で求められる。下記の例で言えば、ある事象Xが条件Yの下で起こる確率、ということになる。
【P(Y|X)】
「P、XギブンY」と読む。Xの条件下でのYの起こる確率、を言う。
【P(X)】
Xの起こる確率
【P(X∩Y)】
X,Yのどちらも起こる確率
このように、異なる確率二つの総合の計算を行うのが、「条件付き確率」である。「Xという条件を満たしたときの、Yの確率」と表現できる。
ここで、「Xを原因」とし「Yを結果」と考えて条件付き確率をとらえる考え方もある。
(2)条件付き確率からベイズ定理へ
ページ目次 [ 開く ]
条件付き確率を、「原因」と「結果」ととらえたときに、その逆が可能になる、すなわち「結果から原因の確率を割り出す」ということを考える。それが「ベイズの定理」である。
と言っても、条件付き確率の数式を変換していくだけで、導き出される。導き出すのは、先ほどの「P(Y|X)」(Xの事象の下でのYの確率)とは逆の「P(X|Y)」(Yの事象の下でのXの確率)である。
Xを「原因」Yを「結果」とするなら、「原因(X)から結果(Y)の確率を求める」のではなく「結果(Y)から原因(X)の結果を求める」となる。
(導出)
・ 条件付き確率の式より、P(Y|X)は
$$P(Y|X)=\frac{P(X∩Y)}{P(X)}$$
これを変形すると、
$$P(X∩Y) = P(Y|X)・P(X) ・・・・・ 式①$$
・ ここで上記の条件付き確率の「X」と「Y」を逆にして、P(X|Y)を考える。すなわち結果である「Y」の条件下で、原因である「X」の起こる確率を導き出す、という言い方ができる。
「この場合、P(X∩Y)はどちらの場合も同じの為、下記の通りになる。
$$P(X|Y)=\frac{P(X∩Y)}{P(Y)}$$
・ これに変形した「P(X∩Y)」(上記の式①)を代入する。
$$P(X|Y)=\frac{P(Y|X)・P(X)}{P(Y)}$$
これが「ベイズ定理」の導出方法である。では、実際の例を見てみたい。
3.問題① 病気の罹患率 ~武漢コロナの罹患率は?~
ページ目次 [ 開く ]
ベイズの定理を考える時に、最もポピュラーな「罹患率」を考えたい。これはまさに武漢コロナに伴うPCR検査を考える時に使える考え方と言える。
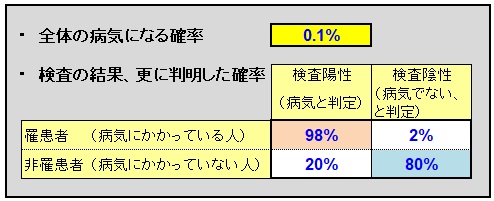
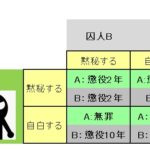
罹患率「0.1%」の病気がある。この病気の検査方法では、
① 罹患した人(病気になった人)で「検査陽性(病気である)」と判定されるのは「98%」だった。
② 罹患していない人(病気でない人)で「検査陰性(病気でない)」と判定されるのは「80%」だった。
ということが分かっている。では、「陽性(病気である)」と判定された人が、本当に罹患している(病気である)確率は何%か?
問題①を表にすると上記のようになる。もし、感覚的に『この検査で「陽性である」と判定された人が「罹患者」である確率』を考えたら、どうなるだろうか?表をパッと見て「98%は罹患している(病気である)」と思ったら間違いである。なぜなら、罹患していなくても陽性となる可能性があるからである。
では、それはどうやって導き出されるのか。そこで「ベイズの定理」の出番である。「罹患した人が検査陽性となる確率」(=98%)等を使って、「検査陽性の人が罹患している確率」を導き出すのである。
罹患を「X」とすると、罹患する確率:
\(P(X) = 0.001(0.1%)\)
検査陽性を「Y」とすると、検査陽性となる確率:
\(P(Y) = (0.001 × 0.98) + ((1 – 0.001) × 0.2)\)
\(= 0.20078\)
罹患している人が検査陽性である確率:
\(P(Y|X) = 0.98(98%)\)
従って「検査陽性の人が罹患している確率 P(X|Y)」はベイズの定理から
\(P(X|Y)=\frac{P(Y|X)・P(X)}{P(Y)}\) より、
$$P(Y]X)=\frac{0.98 × 0.001}{0.20078}=0.00488・・・(0.48%)$$
となる。すなわち、「検査陽性」とされても、この病気とこの検査であれば、本当に「罹患している人」はわずか0.48%ということになる。
この結果はすなわち、「この検査方法だけに頼るのではなく、その後の再検査が重要」ということになる。現在の武漢コロナはで考えれば、PCR検査の結果の見方が見えてくるのではないだろうか?
4.問題①から考えるベイズの定理 ~「事前確率」から「事後確率」へ~
ページ目次 [ 開く ]
先ほどの問題①の意味を再度考えてみたい。
問題①の例では、「原因と結果」という条件付き確率の基本に則して話を進めた。しかし、もう一つの考え方に「事前確率」と「事後確率」とがある。
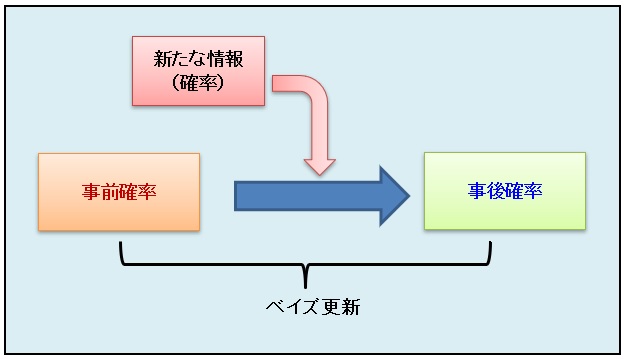
問題①の答えを、「事前確率」と「事後確率」という視点で見ると、下記の通りとなる。
「検査の統計」という情報が加わったことにより、「検査陽性」の人の罹患率が「0.48%」という「事後確率」が得られた。
「原因と結果」という視点もあるが、このように「事前確率」と「事後確率」ととらえるとより分かりやすいと思う。
この問題①の例では、「検査陽性」となってもたったの「0.48%」しか罹患している人はいないのか、と思うかもしれない。しかしこの検査とその統計という新たな情報が加わったことで、「事前確率」が「0.1%」だったものから、5倍近い確率の「0.48%」の「事後確率」が得られたのである。
確かに低いかもしれないが、「検査を行えば、0.1%しかいない罹患者をその5倍の精度で判明できる」、と言える。
このように、新たな確率が加わることにより事象の確率が変わる(更新される)ことを「ベイズ更新」という。
5.問題② AIへの応用を考えよう ~迷惑メールの確率は?~
ページ目次 [ 開く ]
先ほどの問題①は、ベイズ定理を語るときには必ず出る例題だが、今度は、少しAI的な考え方を入れた問題で見てみたい。少し身近な問題で考えると、更に理解が深まると思う。
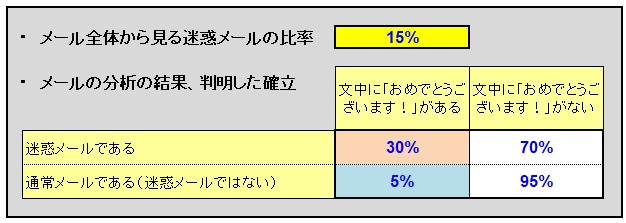
メールの調査で、全体の「迷惑メール」の確率は約「15%」である、という調査があった。
ここで更にメールを分析したところ、
① 迷惑メールの文中で「おめでとうございます!」とあるものは「30%」だった。
② 通常メールの文中で「おめでとうございます!」とあるのは「5%」だった。
ということが分かった。では、「おめでとうございます!」という文字のあるメールのうち、「迷惑メール」である確率は何%か?
問題②は内容はずいぶん異なるが、考え方は問題①と同じである。
迷惑メールであることを「X」とすると、迷惑メールの確率:
\(P(X) = 0.15(15%)\)
メール文中に「おめでとうございます!」とあることを「Y」とすると、その確率:
\(P(Y) = (0.15 × 0.3) + ((1 – 0.15) × 0.05)\)
\(= 0.0875\)
迷惑メールの文中に「おめでとうございます!」とある確率:
\(P(Y|X) = 0.3(30%)\)
従って『「おめでとうございます!」とあるメールが迷惑メールである確率 P(X|Y)』はベイズの定理から
\(P(X|Y)=\frac{P(Y|X)・P(X)}{P(Y)}\) より、
$$P(Y]X)=\frac{0.3 × 0.15}{0.0875}=0.5142・・・・(51.42%)$$
この問題②の計算結果で言える事は、
そこに「おめでとうございます!」というメールの分析結果を加えると、
メール文中に「おめでとうございます!」とあるメールで迷惑メールである確率は「51.42%」であるという「事後確率」が得られた、
という事が言える。この考えに基づいて「迷惑メール」のフィルタリング機能のプログラムが組まれる。メールのフィルタリングに使われる「ベイジアンフィルタ」と言われる技術は、これに「学習」を加え、実際のデータより前提となる確立を修正しながら精度を上げていく。このように「情報をアップデートしながら推定を行う」のを「逐次ベイズ推定」といい、AIの考え方にも多く取り入れられている。
6.ベイズの定理の意味
ページ目次 [ 開く ]
「条件付き確率」の考え方に「原因から結果を導く」という言い方がある。ベイズ定理はそれを「結果から原因を導く」という「逆」ができる、という言い方をするようである。
しかし、私の理解は「事前確率」と「事後確率」という言い方の方が、すっと身に入った。「事前確率」で得られた確率は、更なる調査により得た情報から「事後確率」へと変換(更新)されることで、より正確と思われる確率が得られる、という理解をすると分かりやすいと感じる。この「更新」が「ベイズ更新」である。
7.ベイズの定理を見て
ページ目次 [ 開く ]
ベイズの定理を簡単な例題と共に見てきた。あくまでほんの「入り口」だけの部分ではあるが、方法は理解してもらえたと思う。
しかし、方法は理解しても、ベイズの定理とその計算結果を見てどう思っただろうか?問題①では「検査陽性者の罹患の確率が、たったの0.48%はおかしい!」と思う人もいたと思うし、問題②では「こんな計算でなんで迷惑メールの比率が51%に上がるんだ?」と思う人もあると思う。
私も、特に問題①の結果を見たとき、なぜここまで低くなるのか、少し意外に思えた。
「数学の結果と直感が異なる」ことというのは、往々にしてよくあることではある。この「ベイズの定理」もその一つかも知れない。
しかし、数式上は正しいし、実際にAIにも応用されている考え方である。こうした「数学の結果と直感との違い」を楽しみながら、学んでいけたらと思う。
コメント
この記事へのトラックバックはありません。















この記事へのコメントはありません。